1. sada domácich zadaní

Najneskorší termín odovzdania: 27.2.2022 (nedeľa) o 18:00
Odovzdávané súbory: Fraktalka.java, PoloveAlgoritmy.java.

Doplňujúce požiadavky:

• riešenia, ktoré nebude možné skompilovať (t.j. riešenia so syntaktickými chybami) nebudú hodnotené,
• zdrojový kód správne naformátujte (CTRL+SHIFT+F),
• komentovaný zdrojový kód

Fraktálový trojuholník (1 bod)

V triede Fraktalka, ktorá rozširuje triedu Turtle, vytvorte metódu trojuholnik, ktorá nakreslí fraktál s nasledujúcim tvarom:

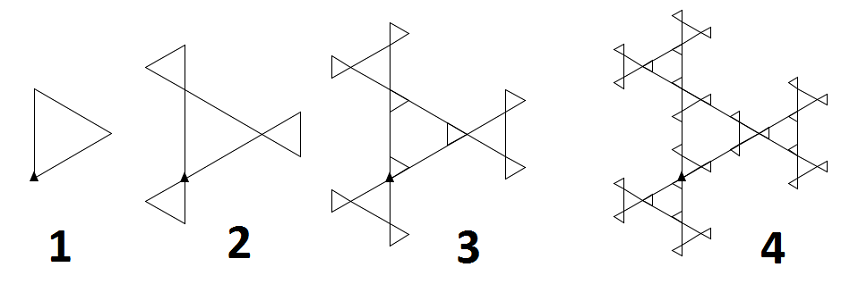
Parameter u určuje "úroveň" fraktálu, parameter d dĺžku strany centrálneho trojuholníka (všetky obrazce na ilustračnom obrázku majú rovnakú dĺžku strany). Korytnačka je na začiatku a na konci na tom istom mieste, natočená je v smere jednej zo strán tak, ako je to na ilustračnom obrázku. Kreslite aj časti fraktálu, ktoré nie je vidieť.

Poznámky:

• V obrázku, ktorý je výsledkom evaluácie v Moodle, je očakávaný výstup nakreslený červenou farbou. V korektnom riešení by ste tak nemali vidieť nič červené, keďže očakávaný výstup je prekreslený výstupom odoslaného riešenia, ktorý je kreslený čiernou farbou.

Polia vo svete bez cyklov (3 body)

Preprogramujte metódu vsetkyRovnake tak, aby robila to isté, ale bez použitia cyklov (while, for), metód JCF a triedy Arrays. Vaše riešenie nech funguje aj v prípade, že vstupné pole je veľké (napr. 1000000-prvkové). Môžete predpokladať korektné vstupy (p != null, 0 <= odIdx <= poIdx < p.length).

Poznámky:

• Pri odovzdávaní triedy PoloveAlgoritmy skontrolujte, že neimportujete žiadne triedy z knižnice JPAZ2, nakoľko tá nie je dostupná pre túto úlohu.
• Preprogramujte = zmeňte len príkazy v tele metódy, t.j. do triedy PoloveAlgoritmy nepridávajte žiadne iné pomocné metódy či statické premenné.

Ammanov šesťuholník - Ammann hexagon, Golden bee (5 bodov)

Aj medzi ľuďmi, ktorí nie sú matematici, sú známe frázy ako: "zlatý rez", "Fibonacciho postupnosť". Kto sa zaoberá hlbšie týmito pojmami a s nimi súvisiacimi časťami matematiky, určite už počul o zlatom obdĺžniku a zlatom trojuholníku, ktoré využívajú tzv. zlatý pomer. No nie je veľa ľudí, ktorí poznajú Ammanov šesťuholník pomenovaný po americkom amatérskom matematikovi. Tento matematik má kľúčový podiel na rozvoji kvázikryštálov a aperiodických pokrývaní roviny. Ide o rovinný útvar, ktorý vieme rozdeliť na dva útvary, ktoré sú s ním podobné. Jednoduchší príklad, ktorý spĺňa túto vlastnosť, je každý pravouhlý trojuholník. Ammanov šesťuholník, ktorý je výsledkom štúdie Ammanovských pokrývaní, bol objavený v roku 1987 Jamesom Schmerlom, ale až v roku 2011 bolo dokázané, že neexistuje útvar s väčším počtom strán, ktorý by sa spĺňal spomínanú vlastnosť delenia. Vedecká činnosť a prezentácie spojené s týmto útvarom vďaka tomu patria k novinkám. Teraz máte jedinečnú možnosť spraviť program na vykresľovanie Ammanovho šesťuholníka, čím sa dostanete približne medzi prvých 100 ľudí na svete, ktorí niečo také naprogramujú. Pritom si môžete všimnúť, že nielen zlatý trojuholník ale aj Ammanov šesťuholník pri tomto delení majú strom volaní rovnakého tvaru ako strom volaní Fibonacciho postupnosti.

V triede Fraktalka, ktorá rozširuje triedu Turtle, vytvorte metódu hexagonAmmann, ktorá nakreslí fraktál s nasledujúcim tvarom:

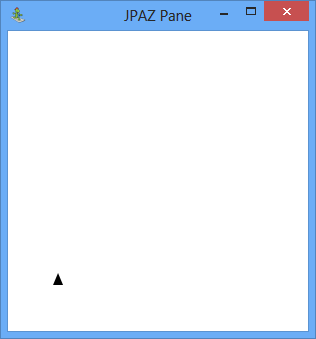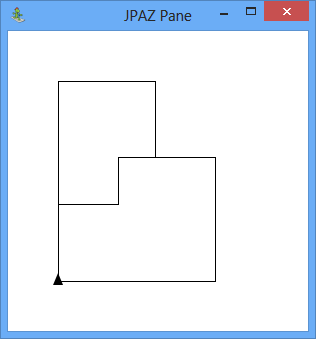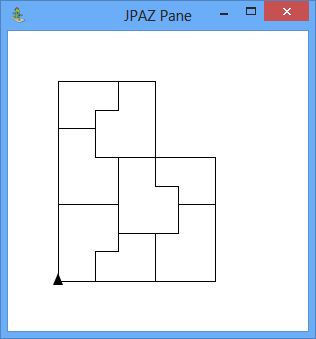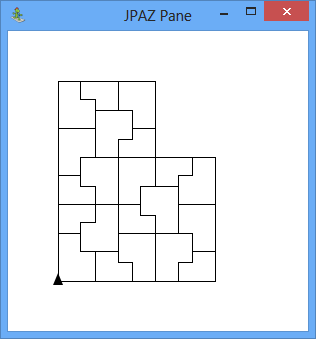
Na obrázku môžeme vidieť úrovne 0 až 7.

Základné rozmery jednotkového telesa pri úrovni delenia 2, pričom Ψ je odmocnina z (√5-1)/2:

Posledný ilustračný obrázok ukazuje úrovne 1 až 3 v prvom riadku, pričom pod nimi sú všetky útvary pri rozložení.

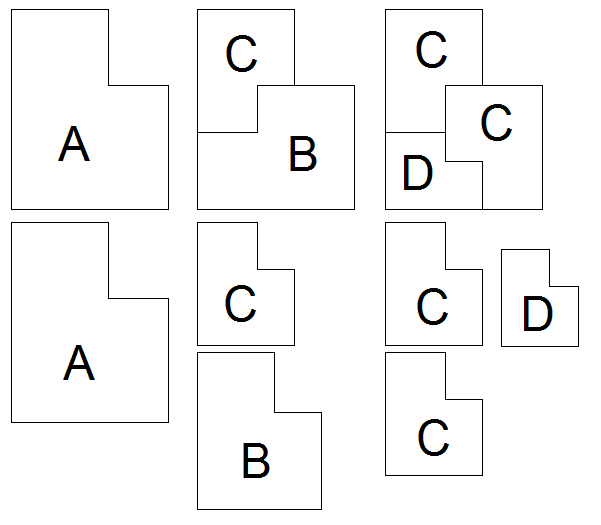
Poznámka: Názov Golden bee bol inšpirovaný tvarom základného útvaru, ktorý dostanete ak ho prevrátite okolo osi x a následne otočíte proti smeru hodinových ručičiek o 90°.

Čítanie pre (nielen) matematikov:

• Zlatý rez a jeho hodnota
• Ammann tilings: a classification and an application