Cvičenia: 1. týždeň

Ciele cvičení:

  • vedieť rozložiť problém na menšie problémy rovnakého typu
    • uvedomiť si, že spôsob rozdelenia ovplyvňuje priebeh výpočtu (maximálnu hĺbku vnorenia)
  • vedieť implementovať rekurzívne riešenie
  • rozumieť vykonávaniu rekurzívneho programu (call-stack a jeho obmedzenie)
  • vedieť schematicky zachytiť výpočet vo forme stromu volaní a analyzovať rekurzívny výpočet

Fraktály

Vytvorte metódy (pridaním metód to triedy rozširujúcej triedu Turtle), ktoré nakreslia nasledujúce fraktály:

public void utvar(int uroven, double rozmer)
[$[Get Code]]

Pred naprogramovaním riešenia najprv spoločne analyzujte fraktál a hľadajte opakujúce sa časti.

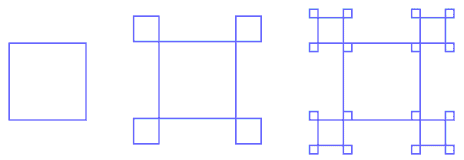
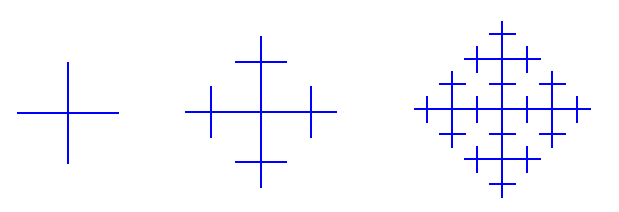
Ďalšie fraktály:

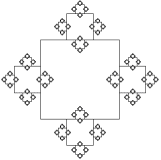
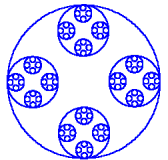
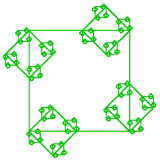
Fraktály "bez úrovne"

Pri kreslení fraktálov zvyčajne špecifikujeme veľkosť fraktálu, ktorý chceme nakresliť. Ak je úroveň fraktálu veľmi veľká, neraz dochádza ku kresleniu podčastí fraktálu, ktoré sú také malé, že "ich nevidno" - napr. sú menšie ako 1 pixel. Pri niektorých typoch fraktálov môže toto pozorovanie viesť k alternatívnemu prístupu, pomocou ktorého "kontrolujeme" zmenšovanie sa problému a vykonanie bázy rekurzie.

public void utvar(double rozmer) {
  if (rozmer < 1)
    return;

  //...
}
[$[Get Code]]

Skúste prerobiť niektoré metódy kresliace fraktály do tejto formy.

Ďalšie fraktály:

Nefraktálova rekurzia a stromy volaní

Využite nasledujúci program na zobrazenie priebehu rekurzívneho výpočtu:

public class TestFibonacciho {

        public static int fibonacci(int n) {
                if (n == 0) {
                        return 0;
                }

                if (n == 1) {
                        return 1;
                }

                int vysledok = fibonacci(n - 2) + fibonacci(n - 1);
                return vysledok;
        }

        public static void main(String[] args) {
                System.out.println(fibonacci(5));
        }
}
[$[Get Code]]

alebo

public class TestFibonacciho {

        public int fibonacci(int n) {
                if (n == 0) {
                        return 0;
                }

                if (n == 1) {
                        return 1;
                }

                int vysledok = fibonacci(n - 2) + fibonacci(n - 1);
                return vysledok;
        }

        // main môže byť aj v samostatnom "spúštači"
        public static void main(String[] args) {
                TestFibonacciho t = new TestFibonacciho();
                System.out.println(t.fibonacci(5));
        }
}
[$[Get Code]]
  • Čím sa líšia vyššie uvedené programy? Vysvetlite.
  • Nájdite v tejto metóde miesta, kde sa realizuje rekurzívne volanie.
  • Vyskúšajte si krokovanie tohto rekurzívneho programu.
    • Aký je obsah call stack-u pred druhým volaním fibonacci(2) ?
  • Na základe analýzy vykonávania programu nakreslite strom volaní metódy fibonacci(4).
  • Porovnajte nakreslený strom volaní so stromom vygenerovaným pomocou knižnice CallTree.
  • Ďalšie úlohy: Doplňte testovací program tak, aby vypočítal (vypísal)
    • Maximálnu úroveň vnorenia pri volaní
    • Celkový počet realizovaných volaní

Rekurzia a polia

  • Zistite pre aké najväčšie pole algoritmus z prednášky na výpočet maximálnej hodnoty v poli skončí bez pretečenia call stack-u.
  • Bez použitia cyklov naprogramujte metódu, ktorá overí, čí čísla v poli int-ov sú usporiadané od najmenšieho po najväčšie.

Strom volaní

Uvažujte takto definované metódy:

public static int fibonacci(int n) {
        if (n == 0)
                return 0;

        if (n == 1)
                return 1;

        return fibonacci(n-2) + fibonacci(n-1);
}

public static int faktorial(int n) {
        if (n == 0)
                return 1;
        else                   
                return n * faktorial(n-1);
}

public static int sucet(int[] p, int odIdx, int poIdx) {
        if (odIdx > poIdx)
                return 0;

        if (odIdx == poIdx)
                return p[odIdx];

        if (odIdx < poIdx)
                return p[odIdx] + sucet(p, odIdx+1, poIdx);
}

public static int sucet2(int[] p, int odIdx, int poIdx) {
        if (odIdx > poIdx)
                return 0;

        if (odIdx == poIdx)
                return p[odIdx];

        if (odIdx < poIdx) {
                int stred = (odIdx + poIdx) / 2;
                return sucet2(p, odIdx, stred) + sucet2(p, stred+1, poIdx);
        }
}
[$[Get Code]]
  • Nakreslite stromy volaní pre fibonacci(6), faktorial(5). Zaznačte aj aké hodnoty sú vrátené v jednotlivých volaniach.
  • Uvažujte pole p = {4, 7, 2, 4, 2, 4, 6, 8, 2}. Nakreslite stromy volaní pre sucet(p, 0, 8) a sucet2(p, 0, 8) vrátane hodnôt vrátených pri jednotlivých volaniach.
  • Čo počítajú jednotlivé funkcie. Vytvorte ich nerekurzívne verzie.
  • Čo viete povedať o jednotlivých stromoch. Aká je maximálna úroveň rekurzívneho vnorenia, koľko volaní je celkovo v jednotlivých stromoch.
    • Špeciálne porovnajte stromy pre sucet a sucet2.
    • Vyslovte hypotézy o štruktúre stromu volaní pre všeobecné vstupné parametre (napr. fibonacci(n), sucet(p, 0, n), sucet2(p, 0, n)).
      • Rada: Do stromu volaní namiesto hodnôt parametrov zaznačte veľkosti uvažovaného vstupu (napr. konkrétne hodnoty poIdx-odIdx+1)
    • Pokúste sa formálne (použitím matematických argumentov, nie len intuície) odvodiť maximálnu hĺbku rekurzívneho vnorenia pri metóde sucet2, ak je vstupné pole veľkosti n
    • Aké najväčšie pole môžeme spracovať metóda sucet a aké metóda sucet2 vzhľadom na obmedzený call stack? (Tvrdenie podporte experimentálnym overením).
    • Ktorej z rekurzívnych metód sucet a sucet2 by ste dali s ohľadom na obmedzený call stack prednosť a prečo?

Poznámka: Pri analýze stromov volaní porovnajte nakreslené stromy volaní so stromami vygenerovanými knižnicou CallTree.

Myslime rekurzívne

Predpokladajte, že máte zakázané používať akékoľvek cykly (while, for).

  • Predpoklad: v rámci podmieneného príkazu if dokážete testovať len rovnosť celočíselnej premennej na 0
    • naprogramujte metódu boolean jeVacsi(int a, int b), ktorá vráti true práve vtedy keď a > b (a a b sú nezáporné celé čísla)
  • Predpoklad: aritmetické operátory okrem ++ a -- sú zakázané
    • naprogramujte metódu int sucet(int a, int b), ktorá vráti súčet parametrov a a b (a a b sú nezáporné celé čísla)
  • Naprogramujte metódu, ktorá spočíta počet výskytov znaku z v reťazci s
    • int pocetVyskytov(char z, String s)
  • Navrhnite metódu (alebo viacero metód), ktorá overí, či 2 polia sú obsahovo rovnaké (rovnaká dĺžka + rovnaké hodnoty v prislúchajúcich si políčkach)
  • Navrhnite, ako by išlo jednoduchý for-cyklus zapísať rekurzívne.

Upozornenie: Vo všetkých prípadoch sú nerekurzívne verzie s využitím cyklov neporovnateľne efektívnejšie. V praxi preto nepoužívať!